这是刷 leetCode 的第四篇博文, 涉及到的题目:
A) 反转字符(编号:344): leetcode-cn.com/problems/reverse-string/
B) 反转字符II(编号:541): leetcode-cn.com/problems/reverse-string-ii/
C) 替换空格(编号:剑指offer 05): leetcode-cn.com/problems/ti-huan-kong-ge-lcof/
D) 翻转字符串里的字符(编号:151): leetcode-cn.com/problems/reverse-words-in-a-string/
E) 左旋转字符串(编号:剑指offer 58 II): leetcode-cn.com/problems/zuo-xuan-zhuan-zi-fu-chuan-lcof/
E) 实现 strStr() 函数(编号:28): leetcode-cn.com/problems/implement-strstr/
F) 重复的子字符串(编号:459): leetcode-cn.com/problems/repeated-substring-pattern/
过程记录
A) 反转字符:
将输入的字符串, 反转过来, 例如: 输入: helloword, 反转后: drowolleh
这题目, 我第一个反应是,把第一个字符和最后一个字符对调, 第二个字符和倒数第二个字符对调…, 其实我们只是遍历一半就可以了。
需要注意的一点是, 遍历的时候, 字符串长度为偶数的话, 直接除以2即可, 但如果是奇数, 需要再加上 1 。
B) 反转字符II:
给定一个字符串和一个整数 K, 每 2k 个字符就把前面的 k 个字符进行反转. 我们可以这样理解, 每隔 K 个字符, 就把接下来的 K 个字符反转过来。
做了前面的字符串反转, 接下来做这个题目就比较容易了, 这个题目其实就是把 2k 个字符进行分组, 把组内的前面 k 个字符进行反转, 我们使用嵌套循环, 外循环用来控制分组, 步长为k, 如果当前循环变量 i % 2 == 0 才允许进入内循环, 内循环用来反转字符, 我们使用双指针, 左指针从左向右移动, 右指针从右向左移动, 然后对调位置, 这样就OK了。
C) 替换空格:
给定一个字符串, 把字符串里面的空格转换成 %20,这个题目, 我的做法是, 定义一个 StringBuffer 变量, 然后变量字符串, 如果是空格, 就把 %20 添加到变量的末尾, 否则把原字符添加到变量的末尾。
这个方面很简单, 网上有些方法先把字符串转换成 char[] 数组来保存, 使用数组来保存的时候产生一个问题, 数组应该定义多长, 做法有两种:
- 先遍历有多少个空格, 根据空格来决定数组的长度, 接着在遍历一遍来替换空格
- 定义的数组长度是原来的 3 倍, 因为在最坏的情况下, 所有字符都是空格, 这样的话, 我们直接把整个数组转换成字符串就可以了, 但是大部分情况下, 不可能所有的字符全是空格, 这样的话我们需要记录有效字符的长度是多少, 然后使用 System.copyOfRange 来拷贝数组
D) 翻转字符串里的字符
给定一个字符串, 将字符串里面的单词出现的顺序翻转过来, 举例子:
“hi , I love you” 变成 “you love I , hi”
解这道题目有两个方法:
- 将字符串分割成数组, 分隔符为空格(“ “), 然后再反转数组里面单词的位置, 前面的反转字符的方法就可以用上了, 再次拼接的时候需要注意的是, 如果单词长度为0, 我们不能拼接上去, 这样就可以了。
- 首先确定字符串左右边界的位置, 这样我们可以把两头的空格去掉, 然后使用双指针从右向左来查找一个单词, 第一个指针确定单词的右边界, 第二个指针用来确定单词的左边界, 获取到单词了以后把拼接到字符串变量里面去, 完成后就得到反转后的字符串了。
E) 左旋转字符串
给定一个字符串和一个整型数值 k, 将这个字符串里面的字符统一向右左移动 k 位, 超出的字符, 把它填补到右边的位置上, 比如:
“hello world” 和 2, 操作后得到 “llo worldhe”
解决办法:
- 截取左边 K 位的字符串, 添加到右边就可以了
- 从左到右遍历字符串的长度, 从 k 位开始遍历, 结束位置为 k + 字符串长度, 遍历位置超出字符串长度时采用取模的方式来解决。
E) 实现 strStr() 函数
给定一个主字符串s, 和模式字符串p, 检查 p 是否是字符串 s 中的一部分, 如果是就返回起始位置, 否则返回 -1。
解这道题目, 我用了两周的时间, 下面给出解决办法:
- 正常思路的算法: 双重循环, 外层循环遍历主字符串 s, 内层循环遍历模式字符串p, 如果完全匹配就返回外层循环的当前指针, 这个简单, 就不多说了.
- kmp 算法:在正常思路的算法中, 其实内层循环会出现重复比较, 导致浪费时间, 而 kmp 算法的思路就是想办法减少内层循环的重复, 这样才能加快匹配的速度, 这里先不做具体的介绍先, 后面我们在做详细的说明
- sunday 算法, 该算法的思路首先跟正常思路的算法一样, 都是需要双重循环, 不同点在于, 当匹配不一致时, 正常思路的算法的外层循环就会向右移动一位, 而 sunday 算法则是一直向右移动, 直到遇到内层循环的不匹配字符时停止, 然后计算内层循环的模式串的第一个字符在主字符串中出现的位置, 接着检查是否完全匹配.
kmp 算法比正常思路的算法快, 具体多少倍不清楚, 而 sunday 算法比 kmp 算法还要快, 但是 sunday 算法比 kmp 算法理解起来要简单得多。
KMP 算法的思路:
假设主字符串为 ababababca, 模式串为 abababca, 现在我们来看下正常思路算法的 gif 动画图

接着我们来看下 KMP 算法的 gif 动画图:
怎么样, 看得出这两个算法的区别了吗?
当两个字符匹配的时候, 正常算法和KMP算法是一样的, 当他们不匹配的时候, KMP 算法能够知道前面的四位是匹配的, 不需要再次比较了, 这样就加快了匹配的速度, 但是, 凭什么 KMP 算法知道前面的4位是相同的呢? 为什么是 4 位而不是 3 位呢?
这里我们引出两个概念: 前缀和后缀。
我们给定一个字符串 hello, 他的前缀就是除了最后一个字符 o 外, 从右到左依次获取到的, 跟最后一个字符相连的字符串, 比如末尾倒数第二个字符l, 还有 ll 等等, 完整的字符串包括{l, ll, ell, hell}。
同样的字符串 hello, 他的后缀就是除了前面一个字符 h 外, 跟第一个字符相连的所有字符串, 都是他的后缀, 比如 e, el, ell, 完整的字符串包括 {e, el, ell, ello}.
我们找出 hello 的前缀集合:{l, ll, ell, hell}, 以及后缀集合:{e, el, ell, ello}, 再找出他们的共同元素, 也就是找出交集: {ell}, 然后从这些交集中找出长度最长的字符串, 该字符串就是 KMP 算法进行比较时, 不匹配的情况下, 前面相同的部分, 当然 hello 这个例子中, 他的交集只有一个: ell, 我们也只能选择该元素了。
再拿 gif 动画图中的主字符串和模式串来举例:
ababababca
abababc
当比较到第7位时(从1开始计数), a 和 c 不一致, 此时前面的字符串是 ababab, 不包括 a和c本身, ababab 的前缀有: {ababa baba aba ba a}, 后缀有: {b ba bab baba babab}, 他们的交集是 : {ba, baba}, 最长的字符串是 baba, 所以他的长度是 4。
这样我们可以根据数字 4, 计算出模式串下一次应该移动到的位置: 4。
为什么这样做就可以确定前面的部分相同, 从而减少比较的次数?
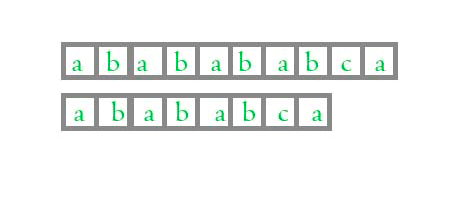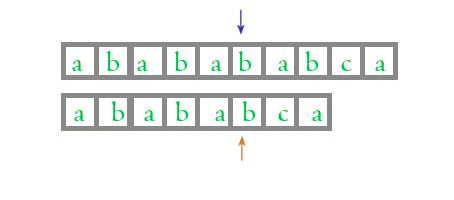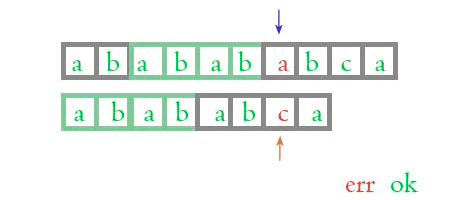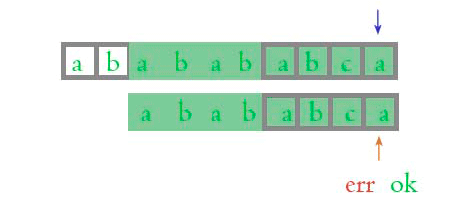
我们再来看下面的这张图片, gif 动画图中显示过, 我们单独拿出来: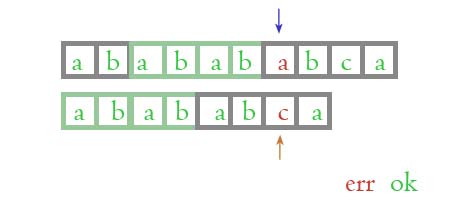
上面的主字符串绿色方框中的 abab, 跟下面的模式串绿色方框的 abab 是不是相同? 肯定相同嘛! 然后我们再来看看前面比较过并且相同的部分: ababab, 针对 ababab 这个字符串来讲, 下面的模式串绿色方框中的 abab 是不是正好位于前面位置? 上面的主字符串绿色方框中的 abab 是不是位于后面位置?
这样比较了以后, 我们就能够明白, 为什么可以忽略过不用再次比较了。
在模式串 abababc 中, 我们举例子正好是在 c 位置不匹配, 因此我们查找的是 ababab 的前缀表和后缀表的交集, 并获取最长的字符串, 但在编码的时候, 不匹配可以在任意位置发生, 因此, 对于模式串 abababc, 我们需要找到所有位置上的交集, 并且获取到最长字符串的长度, 组成的集合表统称为 next 表.
查找 next 表的第二种方法:
上面举例子的时候, 我们用到的方法是查找 next 表的一个方法, 下面再说说另外的方法:
对于任意字符串, 我们都是要查找最长的字符串, 那么, 我们在查找前缀表的时候, 我们可以从右向左找, 查找后缀表的时候可以从左到右找, 只要是匹配了, 他就是最长的字符串了。
比如 hello, 前缀从右向左开始找, 获取最长的部分, 第一次获取到的是 hell, 后缀从左向右找,获取最长的部分, 第一次获取到的是 ello, 然后依次减少位数, 直到位数等于零为止或者获取到匹配字符为止, 下面我们开始模拟这个过程, 这个过程我们忽略掉匹配的字符:
1):
hell o
h ello
2):
ell o
h ell
3):
ll o
h el
4):
l o
h e
很明显, 在第二步骤的时候, 就已经获取到匹配的字符了,因此我们不用 3)4) 这两个步骤了, 这里只是为了理解, 所以把它写出来
查找 next 表的第三种方法:
第三种方法的效率最高, 虽然我可以理解下面这句话, 但是无法理解整个过程:
查找 next 数组的过程, 实际上就是把模式串为主字符串, 把模式串的前缀作为模式串来比较
由于我自己无法想象这个过程, 所以这里就不写了, 请参考这里:
zhihu.com/question/21923021/answer/281346746
他已经画图来表示。
F) 重复的子字符串
给定一个字符串 s, 查找该字符串是否由一个子字符串 t 重复多次构成
网上给出的最简单的思路是: 如果该字符串 s 由子字符串 t 重复多次构成, 那么:
- 去掉s的首尾字符后形成新字符串 A
- A 拼接两次形成新字符串 B
- B 一定包含字符串 s.
下面是另外一种方法:
假定字符串 s 由多个子字符串重复多次构成, 那么它的形式如: axxxmaxxxmaxxxm, 为了方便说明, 它的形式我们做个改变: axxxmbxxxncxxxo, 在这个形式中, a,b,c 一定相同, m,n,o 也一定相同, 因此, 我们采用双指针, 左指针从左向右移动, 右指针从右向左移动, 右指针一定会碰到c, 左指针一定会碰到m, 如果 a == c, 并且 m == o, 那么他有可能符合条件, 这个时候我们检查:
- s 的长度是不是 axxxm 的倍数, 如果不是, 那就继续上面的循环
- 循环检查 axxxm, cxxxo 中的每一个 x 字符是否相同, 如果不相同, 那就不符合条件, 继续上面的循环。
- 循环检查 bxxxn 部分, 看他是否跟 axxm 相同, 如果相同, 那么就符合条件, 否则不符合条件。
总结
字符串匹配查找, 正常的思路不比 KMP 算法快, KMP 又不比 sunday 算法快, 因此我们首先使用 sunday 算法来进行字符串匹配查找。
如果您觉得这篇文章对您的学习很有帮助, 请您也分享它, 让它能再次帮助到更多的需要学习的人. 您的支持将鼓励我继续创作 !